My Hometown is Athens in Greece where I grew up and spent 20 wonderful years. After school, I started my studies as a mechanical engineer in National Technical University of Athens (NTUA). During the studies, I learned many interesting things, but the one which attracted my attention was optimization. This subject combines many sciences such as programming, mathematics, physics and it is a demanding job. Everything can be improved because nothing is perfect, so optimization relevance spans to almost every process to make it operate more efficiently and effectively. My diploma thesis was dealing with aerodynamic optimization using the continuous adjoint method in OPENFOAM. After the studies, I completed my military service. Then, I returned to the Parallel CFD & Optimization Unit in NTUA for 9 months to train myself with OPENFOAM and to broaden my knowledge in the area of continuous adjoint method.

In April, I started working for Engys Ltd. in London as a PhD student. AboutFlow project gave me the opportunity to work in industry as a researcher in optimization and specifically in adjoint methods. My research is dealing with the topology optimization using the continuous adjoint method in OPENFOAM. The main objective is the development of the level-set method with immersed boundaries inside the current optimization engine of Engys. In addition, the accuracy of the code will be improved using adjoint turbulence. Furthermore, a multi-objective optimization tool will be developed for the creation of a Pareto Front. The last part of the project consists the multi-point optimization. A code for handling multiple primal inputs fields, which will be running concurrently with the adjoint evaluation, will be developed. These features will be used from people in industry and will be tested in industrial cases for topology optimization.

Without any doubt, AboutFlow project is a great opportunity for me. The fact that my work will be used directly from the people in industry is really interesting and gives me extra motivation. Communicating with the partners and generally with the CFD community at conferences and workshops is really interesting experience for me.

Objectives:

• Improve the modelling accuracy and quality of the immersed fluid/solid interface

• Develop an efficient adjoint topology optimisation method that will produce shapes that are robust to a range of operating conditions

Contribute to Work Packages

• WP 1
• WP 2
• WP 5
• WP 6

One of the fastest growing fields in CFD is adjoint optimization. The method has started to find its way into industry, where it is being used to optimize various products. Drag force minimization of a car, lift force maximization of aircraft wings and minimization of power losses in HVAC ducts are some typical optimization problems being so treated.

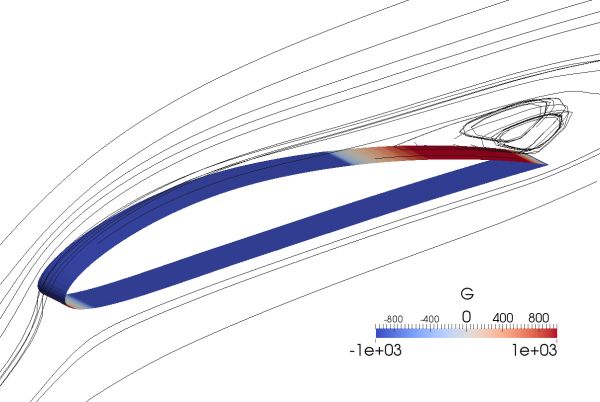
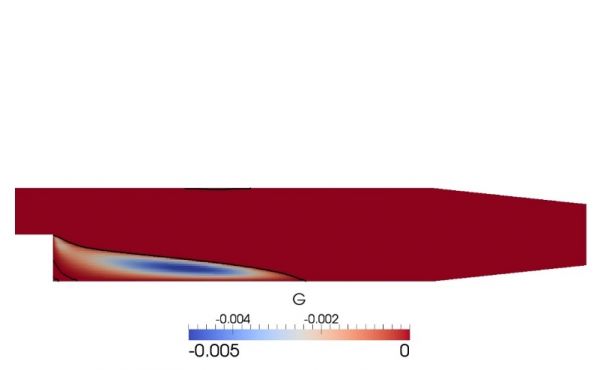
Adjoint methods can be used for calculating surface (Figure 1) or volumetric sensitivity (Figure 2) derivatives of objective functions (drag-lift force, power losses, mass flow split, etc.). The main advantage of adjoint methods comparing with other techniques (evolutionary algorithms, direct differentiation, etc.) is the efficiency.

Figure 1: Surface sensitivities of a wing. Red areas - Push out, Blue areas - Push in.	Figure 2: Volumetric sensitivities on a backward facing step.

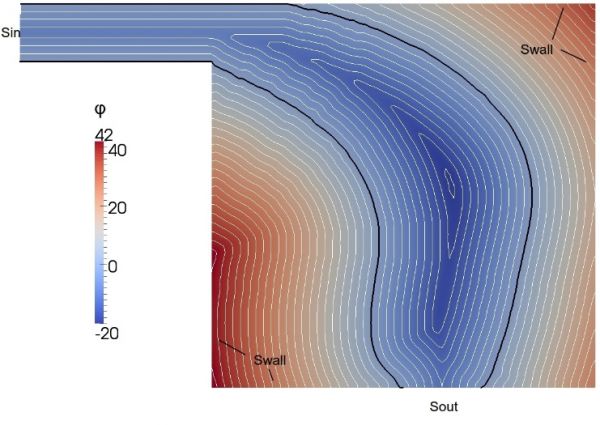
Figure 3. Level-set field on a 2D Case. Negative and positive areas are fluid and solid areas respectively.

My project is dealing with the level-set based topology optimization using the continuous adjoint method [1]. The level-set method is inspired from a paper of J.A. Sethian [2], which details the use of the level-set method as a tracking interface and is made up of three parts: velocity extension, evolution, reinitialisation. The level-set method is generally categorized in the topology optimization but in fact it is using some elements of shape optimization. The design variables in the level-set method are the signed distances (Figure 3) between the cell centers and the interface. As a result, the zero level-set contour is the interface (for example the surface of the duct). Immersed boundaries are imposed on the interface in order to model it as it is a wall boundary. Curvature is calculated as the laplacian operator of the design variables and is used as an additional objective for curvature minimization. Curvature objective is making the optimized surfaces smooth and manufacturable.

Applications

1. HVAC Cooling Duct

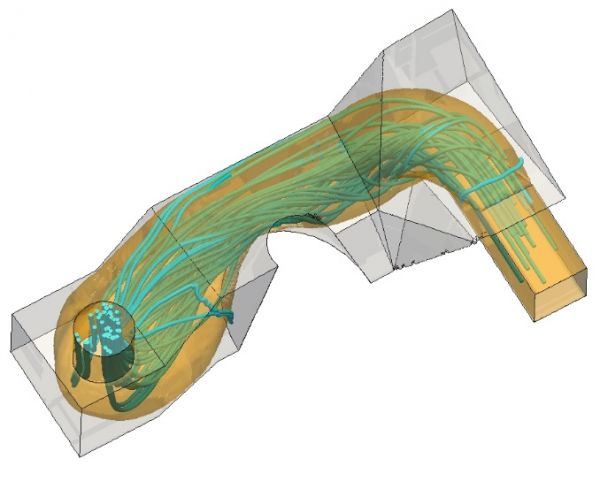
Figure 4. Topology optimization of a HVAC cooling duct using the level-set method. The grey and yellow surfaces are the baseline and optimized surface respectively. It is clear that the recirculation zones which appeared in the flow of the baseline mesh, are not present after the optimization. The objective function (power losses) are decreased 50.65% after the optimization.

2. Gear Pump

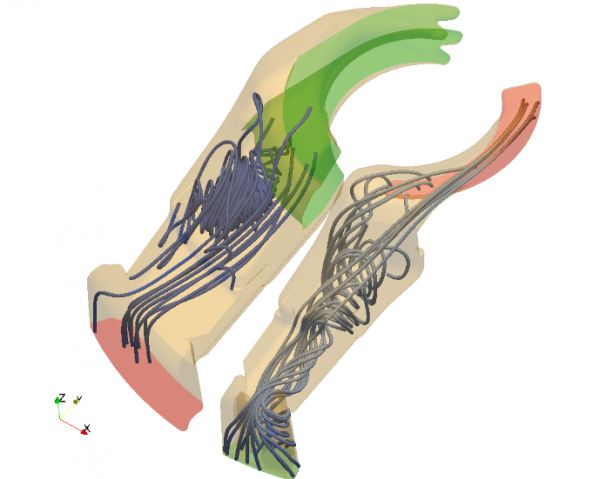
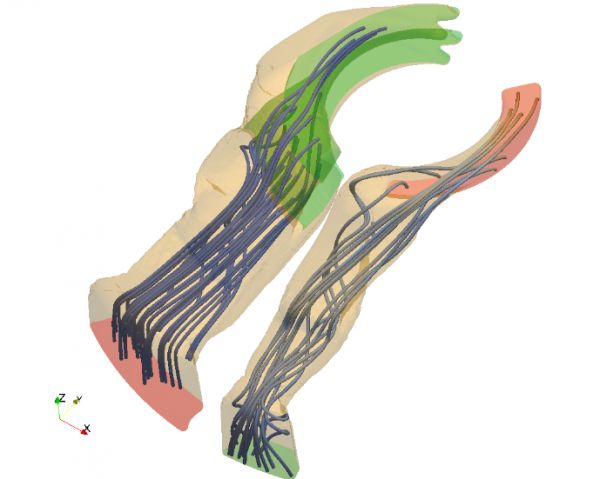
Figure 5. Topology optimization using the level-set method in a gear pump. The whole gear pump is separated in two different cases: the inlet port and the outlet port. The objective function (power losses) are decreased 22.5% after the optimization. The geometry is provided by Aisin AW.

1.  Georgios K. Karpouzas,Evangelos M. Papoutsis-Kiachagias, Thomas Schumacher,Eugene de Villiers,Kyriakos C. Giannakoglou,Carsten Othmer:Adjoint Optimization for Vehicle External Aerodynamics,International Journal of Automotive Engineering, Vol.7,No.1,pp.1-7(2016)
2. G.K. Karpouzas, E.De Villiers: Geometric Immersed Boundaries (GIB): A New framework for applying boundary conditions in OpenFOAM®, ESI OpenFOAM User conference 2015 - Best presentation Award
3. G.K. Karpouzas, E.De Villiers: Adjoint optimization for external aerodynamics, OpenFOAM Workshop 2015
4. G.K. Karpouzas, E.De Villiers, D.P Combest: Leaveraging the continuous adjoint method for industrial scale application, NAFEMS 2015.
5. G.K. Karpouzas, E.De Villiers, T. Schumacher: Adjoint optimization with Helyx, NOFUN 2014
6. G.K.Karpouzas, E.De Villiers: Industrial application of an adjoint level-set based optimisation method, OpenFOAM Workshop 2014
7. G.K.Karpouzas, E.De Villiers: Level-set based topology optimisation using the continuous adjoint method, Opt-i 2014
8. G.K.Karpouzas, E.De Villiers: Level-Set based Topology Optimisation using Adjoint CFD, OpenFOAM Workshop 2013

References

1. A.S. Zymaris, D.I. Papadimitriou, K.C. Giannakoglou, and C. Othmer. Continuous adjoint approach to the Spalart-Allmaras turbulence model for incompressible flows. Computers & Fluids, 38(8):1528–1538, 2009.
2. J.A. Sethian. Evolution, implementation, and application of level set and fast marching methods for advancing fronts. Journal of Computational Physics, 169:503–555, 2001.

My outreach activity involves a presentation in London or British science festival of 2015. It will be a visualization on how can some numbers or equations can be translated to colours on a car or an aeroplane and how this can be useful for the engineers.

This activity is aiming to engage teenagers who they find images with racing cars or the complexity of the equations fascinating. In addition, if other researchers from different fields, find something interesting in my research, they can be engaged.

The first part of the presentation will include some videos and images with some simulations I made for my research. The second part, I will show the equations I solved for these simulations.

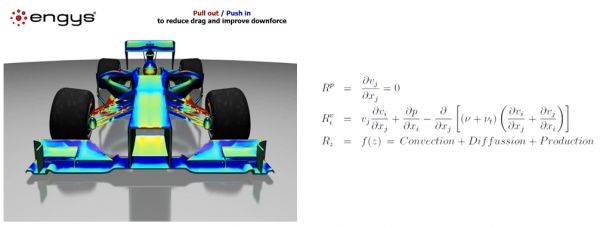
The goal of this presentations is to motivate the young people to become engineers in the future and make them understand the value of mathematics, physics and computers on everything around us. Also, the other engineers can also check my work on the internet and they can find something that is useful to their research.

The whole activity requires some time for the preparations. The work load is divided in four parts:

1. Extraction of the eye-catching images/videos (1 week),
2. Writing of the equations (1 week)
3. Preparations before the festival (1 week)